Programme National d'Innovation 97-99. (PNI 2)
ECRIRE UN PROGRAMME DE CONSTRUCTION
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Depuis peu, on constate que, dans les discours officiels, on a substitué l'expression "maîtrise des langages" à celle de "maîtrise de la langue" Ce glissement peut paraître anodin au premier abord, mais il prend réellement du sens si l'on considère les relations que les apprentissages disciplinaires entretiennent avec la langue. Se donner comme objectif la "maîtrise de la langue" amène à considérer l'apport de chaque enseignement disciplinaire au développement des compétences langagières (à l'écrit ou à l'oral). Permettre la "maîtrise des langages" invite plus précisément les enseignants à identifier "les langages" propres à chaque discipline et à favoriser leur apprentissage. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Encore faut-il définir ce que sont les langages. Les mathématiques, par exemple, ont recours à des codes multiples : écritures symboliques, graphiques, tableaux, schémas, figures géométriques et langue naturelle, laquelle propose un vocabulaire spécifique et des acceptions "mathématiques" de certains éléments du lexique usuel (sommet, hauteur …). Par ailleurs, les écrits propres à cette discipline adoptent souvent des organisations syntaxiques particulières (c'est le cas, par exemple, des énoncés de problème, des propriétés, des textes de démonstration …), autant de "faits langagiers" qui sont constitutifs de ce champ disciplinaire. Ces nombreux modes de représentations, les passages fréquents de l’un à l’autre (par exemple : à partir d’un texte, construire une figure, ou un graphique, ou inversement…) nécessitent un véritable apprentissage pour devenir des outils efficaces. Il est également possible de considérer que la démonstration, la justification… sont également, en mathématiques des situations langagières particulières qui sollicitent des compétences spécifiques. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La géométrie se prête particulièrement à l’articulation entre activités langagières et apprentissage mathématique. C’est un domaine riche pour imaginer des situations d’écriture et de réécriture variées. Dès les premières années de collège, la géométrie est présentée de façon très différente par rapport au point de vue adopté à l’école primaire. Les représentations que se font les enfants des objets géométriques doivent donc évoluer : faire écrire les élèves permet à l’enseignant de savoir où en est chacun, et leur faire confronter les différents écrits produits dans la classe, en vue d'une réécriture mieux contrôlée, va les aider à changer le regard qu’ils portent sur les objets de la géométrie . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
« Plus jamais je ne leur ferai écrire des textes de mathématiques, je ne sais qu’en faire !" Voici une réflexion que pourrait faire un collègue de mathématiques en salle des professeurs. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Des exercices de description de figure sont souvent proposés aux élèves dans les évaluations nationales de début de sixième. Malgré le codage imposé, qui n’a pas éprouvé des difficultés à évaluer certains textes produits par les élèves ! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les programmes de sixième suggèrent de travailler selon le principe des figures téléphonées[1] pour passer du "faire" au "faire faire" [2].. On peut cependant observer que les élèves se comprennent parfois sans que leurs textes soient acceptables du point de vue de la précision mathématique et du vocabulaire utilisé ! Qui ne s’est alors demandé : que faire de ces textes, comment faire comprendre aux élèves que cela n’est pas suffisant même - et surtout - s’ils ont réussi à reproduire une figure avec un texte imprécis ? Il est possible de juger cette communication efficace, mais nous nous apercevons souvent que les textes écrits ne sont pas satisfaisants du point de vue des mathématiques et peut-être pas davantage du point de vue de la langue. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les programmes de sixième suggèrent aussi "d’entraîner les élèves à mieux lire et mieux comprendre un texte mathématique, et aussi à produire des textes dont la qualité est destinée à être l’objet d’une amélioration progressive". Il est donc nécessaire de proposer des activités qui permettraient aux élèves de produire et surtout d’améliorer des textes. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les séances qui vont être décrites en détail visent à faire écrire des textes de construction de figures à des élèves de sixième. Le travail part du constat que la majorité des élèves n’écrit pas des textes satisfaisants même si des modèles ont été utilisés en lecture pendant la leçon ou les exercices d’application. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Par une étude critique de petits textes de l’évaluation de sixième produits en début d’année, les séances proposées ci-après visent l’appropriation de critères et la construction d’une fiche d’aide à l’écriture de programme de construction de figures ; le support de l’activité fait intervenir la notion de cercle. Pour la construction de cette fiche, les élèves sont amenés à repérer des caractéristiques de textes " experts " visant à faire construire une figure, puis ils utiliseront ces critères sur des exemples. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dans l’exposé de notre travail, nous chercherons plus à décrire l’activité comme une activité transposable à partir d’autres textes élèves (ceux de ses propres élèves) plutôt que comme un produit fini à utiliser tel quel. Le travail mené avec les élèves s’inscrit dans un processus d’écriture, réécriture. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dans un premier temps, nous exposerons les objectifs et la construction de l’activité par l’enseignant, puis dans un deuxième temps, nous détaillerons ce qui s’est passé en classe. Nous renvoyons le lecteur aux annexes pour prendre connaissance des fiches élèves. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
En vue de faire "produire des textes dont la qualité est destinée à être l'objet d'une amélioration progressive" (extrait du programme de sixième), nous avons défini les objectifs suivants : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Objectifs de l'activité : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Prendre conscience de la nécessité d'un langage précis. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Repérer des caractéristiques d’un texte expert. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Définir des critères pour évaluer son texte de programme de construction. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· Savoir définir le cercle par son rayon et son centre ou par son diamètre. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Place dans la progression : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Au début du second trimestre, en géométrie, les élèves ont travaillé auparavant sur les notions et thèmes suivants : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· les droites parallèles et perpendiculaires, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· les notations des droites, demi-droites, segments et de longueurs, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
· les reports de longueurs, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
·
à partir d'un texte, d'un dessin à main levée, d'une
copie réduite... des constructions de dessins avec parallèles,
perpendiculaires, cercles, triangles, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
·
le cercle et le vocabulaire associé. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Description de la suite des séances : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Première
séance : (sur deux heures de cours)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1h. Présentation, mise en route et travail de groupes. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1h. Comptes-rendus par les élèves du travail de chaque groupe. Avec l'enseignant "regroupement des phrases exprimant une même chose". Synthèse écrite dans le cahier. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deuxième
séance :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1h. Comparaison d’un "texte professeur" et d’un "texte élève" en vue d'améliorer l'écriture et de prendre conscience des caractéristiques d'un texte "expert".[3] |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Troisième séance :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1h. Rédaction par les élèves de programmes de construction de figures composées de cercles et de carrés en utilisant le travail précédent, et évaluation. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Au moment où se place l’activité (début du second trimestre), les élèves ont déjà lu des textes et exécuté des figures et ont pu se créer des modèles implicites de textes visant à "faire faire". Travailler sur les textes écrits par les élèves permet à l'enseignant de diagnostiquer leurs connaissances des objets de la géométrie et les conceptions qu’ils en ont. Quand par exemple, un élève parle de "rond de 8 cm de longueur et 8 cm de largeur", derrière son propos, on peut imaginer une représentation où le cercle est inscrit dans un carré. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Comme la production de textes mathématiques et en particulier la description de figure est un exercice très mal réussi dans l'évaluation de sixième, nous avons étudié un corpus de 35 réponses de 44 élèves (certains élèves n’ont pas répondu ou ont refait la figure). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L’exercice est le suivant : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
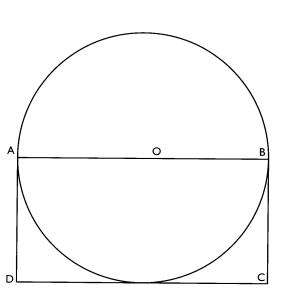 |
Complète le texte ci-dessous, qui doit permettre de
reproduire la figure tracée. Trace un rectangle ABCD de longueur 8cm et de largeur 4cm.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nous avons effectué un choix dans les réponses élèves à partir de critères des textes injonctifs : exhaustivité (il ne manque rien, il y a toutes les informations pour réaliser la figure, il n’y en a pas trop…), exactitude (les informations données sont exactes, précises du point de vue du vocabulaire utilisé, des notations, des expressions mathématiques…), clarté et ordre (du point de vue de la chronologie de la construction). Examinons maintenant sept réponses d'élèves à l’exercice choisi, auxquelles nous avons ajouté deux "bonnes réponses". Nous allons faire une analyse rapide des réponses retenues (les prénoms ont été changés pour éviter des commentaires de la part des élèves et l’orthographe a été rétablie) : Pierre : Prendre le
milieu de la longueur du rectangle puis, placer un point O. Tracer le cercle
passant par A et B. Jacques : Place le
point O au milieu du segment [AB]. Trace le cercle de centre O et de rayon 4cm. Vincent : Trace un
rond de 8 cm de longueur et 8 cm de largeur, place sur le rectangle, avant de
faire le rond, le point O qui est au milieu à 4 cm. Laurence :Tu vas à
la ligne AB et tu fais un point O. Tu prends ton compas et tu fais un cercle de
4 cm. Denise : Place ton
compas sur le centre O, trace ton cercle. René : puis tracez un
cercle dont le point O est le centre et qui passe par les points A et B. François : Appelle
O le milieu du segment [AB]. Trace le cercle de diamètre [AB]. Hervé : Trace un
rond de milieu O qui est à la moitié de A et de B. Laetitia :Trace un
cercle qui a pour centre le point O. Ce cercle a 8 centimètres de rayon. Les réponses de Jacques et de François sont des "bonnes réponses" ajoutées par l’enseignant. Beaucoup de ces textes ne sont pas exhaustifs, ils sont inexacts par l’utilisation d’un vocabulaire non géométrique ou une mauvaise utilisation des notations. La position du centre du cercle est rarement mentionnée explicitement. L’ordre de construction n’est pas toujours respecté. La phrase de Pierre n’est pas très claire et contient des implicites (O est le milieu de [AB] et O le centre du cercle), on peut remarquer que la longueur du rectangle est utilisée comme segment et non comme une mesure (polysémie du mot longueur). La réponse de Vincent montre que le concept de cercle n’est pas acquis (longueur largeur, pas de centre ni de rayon), l’ordre d’exécution n’est pas respecté. La réponse de Laurence contient des implicites sur la position du point O en tant que milieu et en tant que centre du cercle. Cette phrase aurait pu être éliminée car l’analyse rejoint celle de la phrase de Pierre. Denise ne tient pas compte du destinataire qui n’a pas la figure et oublie de donner le rayon. La construction de la phrase de René montre que cet élève a une certaine maîtrise du français mais il oublie de tenir compte de ce que sait déjà le destinataire du message (il ne connaît ni l’existence ni la position de O). La réponse d’Hervé n’utilise pas le bon vocabulaire et ne précise pas le rayon du cercle. Laetitia se trompe de mesure pour le rayon ou de vocabulaire (confusion entre rayon et diamètre), elle ne donne pas la position de O.
À
partir de cette sélection, nous avons proposé aux élèves d’analyser des
réponses en leur donnant le support suivant :
En préalable (juste avant l'activité), nous avons donné à refaire le
texte de description de figure de l'évaluation de début d'année. À la fin de la
première séance, les groupes qui ont terminé l'analyse avant les autres ont
reçu comme consigne de critiquer leurs textes. Première séance :Pour rechercher ce qui va et ce qui ne va pas dans les textes proposés, les élèves ont été mis en groupes de 3 ou 4. Un élève, choisi au hasard dans chaque groupe, a présenté le travail du groupe au reste de la classe. La production du groupe a été recopiée par leurs auteurs sur une grande affiche et ces affiches sont restées au mur pendant la deuxième séance où, avec l’aide de l’enseignant, les élèves ont indiqué "les phrases qui veulent dire la même chose". L’enseignant a recopié les phrases, mais il aurait été certainement plus judicieux de les entourer de couleurs différentes directement sur les affiches. Observation et commentaires sur le déroulement :Au début, les élèves reproduisent des commentaires de professeur comme “révise”, “bien”, “moyen”, “tu es incompréhensible”, “vous ne savez pas vous exprimer”, “juste mais...”, “bien mais pas assez précisé”... . En fait, le "tu vas remplacer le professeur" de la consigne les invite effectivement à ce genre d’attitude, ce qui en dit long sur les représentations qu’ont les élèves du travail de correction d’un professeur ! Ces commentaires renvoient à un jugement de valeur sans qu’il y ait des points d’appui pour une correction ou des conseils de réécriture. On pourrait penser qu’il serait judicieux de changer la consigne mais il est aussi intéressant que les élèves se rendent compte que nous leur demandons d’aller plus loin dans l’analyse (le temps à consacrer à ce travail est important et il ne faut pas le réduire, au risque de n’avoir que ce type de commentaires). À la question de préciser ce qui ne va pas, les élèves repèrent bien les défauts et les critères que nous cherchons à faire ressortir. Ceux-ci apparaissent de manière importante pour ce qui concerne les informations nécessaires (exhaustivité) et les informations justes (exactitude) et de manière plus restreinte pour ce qui relève de la clarté ou de la précision et de l’ordre. Commentaires d’élèvesPour éclairer notre propos voici une suite de commentaires d’élèves qui concernent les informations nécessaires, les informations justes (mesures, vocabulaire, expressions de géométrie…), l’ordre et la clarté : Informations nécessairesil manque des choses- il manque une phrase- phrase incomplète- il manque le milieu du diamètre- à 4cm de quoi ?- tu ne précises pas où est le point O et tu ne précises pas que le cercle est de centre O- combien de rayon ?- quel est le rayon ?- ne dis pas où est le centre- où est O ?- quand tu le dis une fois, tu n’as pas à le dire 2- je te conseille de donner les dimensions. Pour la réponse de Jacques, les élèves la désignent tous comme la meilleure en précisant : la meilleure parce qu’il donne tout pour faire le dessin ; il n’oublie rien car le rayon est bien de 4cm et le point O est bien au milieu de [AB] ; excellent tu précises bien tu emploies les bons mots grâce à ton explication la personne qui veut reproduire cette figure pourra le faire avec précision. Informations justes :je
te conseille de changer de mots- tu n’utilises pas les bons mots- pas juste
parce qu’elle ne donne pas de dimensions- le cercle n’a pas 8cm de rayon
mais 4cm- on ne dit pas rond mais cercle- le cercle n’a ni largeur ni
longueur- mesures pas bonnes- un cercle de 4cm de quoi ? on ne dit pas
ligne mais segment ou longueur- problème de codage : diamètre AB
(François)- un diamètre n’a pas de lettre mais 8cm- ce n’est pas une
longueur ici mais un segment (François)- utilise le langage mathématique- où
places-tu ton compas ? longueur : mal employé. Ordre :souvent les phrases ne sont pas dans le bon ordre (Pierre)- pour Vincent il faut mettre les phrases dans l’ordre- pour René d’abord il faut placer le point O et après faire le cercle. Clarté :pour Jacques sa phrase est très claire- à 4cm de quoi ? -imprécis quand il dit longueur du rectangle laquelle ? assez long ta réponse- des fois, on ne comprend pas ce qu’il veut dire- la meilleure c’est celle de Jacques, car il explique très bien. À la suite de la mise en commun, les élèves ont
élaboré avec l’enseignant le texte ci-dessous pour faire la synthèse du
premier travail. Celui-ci est écrit dans le cahier de leçon : Pour écrire un texte de construction de
figure, *
il ne faut pas oublier d’informations, ni en mettre trop, *
il faut que les informations soient dans le bon ordre, (pour faire faire la figure) *
il faut mettre les bonnes mesures, utiliser le bon vocabulaire et le bon
codage. Deuxième séance :Il est clair pour chacun de nous qu'un texte "expert" a d’autres caractéristiques, nous avons donc prolongé ce travail. Pour que nos élèves de sixième en prennent aussi conscience, nous avons utilisé une activité de la brochure de l’IREM de Rennes "Lire et écrire des textes mathématiques. Vers la rédaction de démonstrations" (voir annexe 1). Cette activité comporte deux fiches élèves. Dans la première fiche, les élèves doivent construire une même figure en utilisant soit un texte élève, soit un texte professeur (ils ont le choix). Dans la deuxième fiche, en comparant les deux textes (en les mettant en regard, phrase par phrase) les élèves sont amenés à essayer de caractériser un texte professeur. Les auteurs de la brochure ont retenu pour un texte professeur les six caractéristiques suivantes : · le texte est dépersonnalisé · la description de la figure ne se fait pas en terme de mouvements · le texte ne mentionne pas l’outil utilisé · le vocabulaire mathématique est utilisé systématiquement · les relations entre objets mathématiques sont favorisées[4] · cette description ne se fait pas grâce à un repérage par rapport à la feuille de papier. Observation et commentaires sur le
déroulement :
La construction de la figure est bien réussie par l’ensemble des élèves. Certains utilisent seulement le texte professeur, d’autres le texte élève, avec des allers-retours vers le texte professeur quand l'un des deux textes ne leur paraît pas clair. Il est à noter que, sur l'ensemble des deux classes, deux élèves n’ont pas compris la consigne et vont essayer de faire deux dessins, un pour chaque texte. Dans le contexte de cette comparaison de textes, la question de la fiche 2 "Est-il nécessaire de donner le nom de l’instrument utilisé ?" n’a pas été bien comprise : bien que certains aient écrit "pour tracer un cercle nous devinons qu’il faut utiliser le compas", beaucoup ont quand même répondu OUI. Malgré les différentes questions de cette fiche, les élèves ont eu beaucoup de difficultés à repérer des différences entre les deux textes. Ils repèrent facilement ce qui ne va pas dans le texte élève, mais ils n’arrivent pas à exprimer de façon plus générale les caractéristiques du texte professeur, à savoir : · emploi systématique d’un vocabulaire mathématique sans préciser les instruments à utiliser, sans décrire tous les gestes effectués, contrairement à un texte élève, · liste de constructions élémentaires (non spécifiées, dépersonnalisées) et non description d’actions, comme le texte élève. En effet, on doit savoir que le lecteur mathématicien déduira les scripts d’action à partir du résultat à obtenir. Ce qui distingue ce type d’écrit d’autres textes (de type injonctif) que les élèves ont l’habitude de manipuler (recette de cuisine par exemple). À la suite de ce travail, une fiche d’aide à l’évaluation d’un texte de construction (où apparaissent les critères déjà cités) est fournie par l’enseignant (mais elle a été déjà, en partie, constituée avec les élèves), puis elle est utilisée pour écrire d’autres textes de construction de figure. Une première version de cette fiche faisait apparaître des phrases négatives comme "je n’ai pas indiqué les instruments utilisés", formulation qui a mis certains élèves dans l'embarras lorsqu'il s'est agi pour eux de répondre par OUI ou par NON. Une dernière version, qui sera définitive, inclut trois critères non-mathématiques : l’orthographe, le mode et temps des verbes et la présentation. La fiche présentée en annexe 2 est le résultat d’un travail réalisé en plusieurs étapes, mais nous n’avons pas fait apparaître de séparation entre ce qui relève du mathématique et ce qui est plutôt de l’ordre du contrat pédagogique. On pourrait penser qu’il aurait été judicieux de distinguer plus nettement ce qui relève de l’exigence mathématique d’une part (en faisant apparaître les critères d’exhaustivité, d’exactitude, d’ordre et de clarté …) et ce qui paraît plutôt relever de la maîtrise du français (orthographe, énonciation, présentation d’un texte…) d’autre part. Mais il nous semble justement que l’énonciation, par la prise en compte d’un destinataire, permet à l’élève de veiller à ne rien oublier, de respecter un ordre de construction et un vocabulaire mathématique. Enfin, le fait de revenir à la ligne pour chaque instruction est un moyen de prendre en compte les critères d’ordre et de clarté, caractéristiques de ce type de texte mathématique.
Troisième séance : Pour tester l'efficacité de la fiche de critères et entraîner à son exploitation, la quatrième heure est consacrée à un travail d’écriture. On propose aux élèves plusieurs figures, composées chacune d'un cercle et d'un carré ; ils doivent alors écrire un texte de construction, le vérifier à l'aide de la fiche et le rendre à l’enseignant. (voir Annexe 3). L'analyse de cette 3e séance montre qu'il n’est pas nécessaire de proposer des figures complexes avec des programmes de construction trop longs ; par contre, il est essentiel qu’il y ait une relation entre les objets mathématiques et il est intéressant qu’il y ait plusieurs constructions possibles (faire le carré puis le cercle ou inversement). Les textes à écrire étant a priori courts, la vérification se fait assez rapidement et facilement.
Il est à remarquer que la leçon sur le cercle avait été faite. Les élèves avaient donc des modèles d’écriture dans les exercices de constructions et dans la leçon. Cependant, l'activité préalable d'écriture d'un premier texte de construction (celui de l'évaluation) a montré que ces modèles n’avaient visiblement pas été acquis par la majorité des élèves. En revanche, à l'issue des quatre séances décrites, tous les élèves sauf un ont réussi à produire des textes corrects, c’est-à-dire qui correspondent aux critères énoncés plus haut. Il ressort de ce travail une certaine satisfaction tant pour l’enseignant que pour les élèves. En effet, il a favorisé une évolution visible des représentations des élèves, mais surtout il leur a permis de prendre conscience de leurs progrès au fur et à mesure que les textes étaient écrits et, par ce fait, il a créé une certaine motivation. En fin de sixième, les textes des élèves ne sont bien sûr pas encore des textes parfaits, mais une meilleure prise en compte d’un destinataire (imaginaire ou non) est faite et les critères d’exhaustivité, d’ordre et d’exactitude sont mieux compris et respectés. Les textes ne sont plus des textes de description (il y a, à gauche en haut...), mais sont bien devenus des programmes de constructions avec des ordres donnés (tracer, placer, appeler...). Les élèves se sont construit ces représentations d’un programme de construction par la confrontation à des textes experts, la comparaison à leurs propres textes, avec l’aide de l’enseignant, mais sans que celui-ci impose un formalisme rigide. Un bénéfice de ce genre d’activité est qu'il donne du sens à un travail d’écriture et de réécriture : on peut revenir sur un texte, le retravailler pour qu’il soit plus compréhensible... On peut craindre que les élèves se lassent vite, qu’ils ne veuillent pas reprendre leurs textes car souvent, pour eux, un travail rendu est fini, on n’y touche plus. Les textes doivent donc être très courts et les figures, tout en étant différentes, se ressembler suffisamment pour permettre des réinvestissements sur des supports différents. Ce travail avec les élèves prend du temps (beaucoup !), mais c'est un investissement à long terme. Repérer avec les élèves les caractéristiques des textes mathématiques est essentiel, car, d’eux-mêmes, les élèves ne sont pas tous capables, par mimétisme et adhésion à un modèle, de s’approprier ces critères. Ces activités sont utiles aux élèves, car elles favorisent une mise à distance des textes et des figures correspondantes, et nous espérons qu’en quatrième, quand ces élèves aborderont la démonstration, ils maîtriseront mieux le langage mathématique et seront capables d’effectuer des allers-retours entre le texte et la figure. Ecrire et réécrire, ce n’est pas réservé à la classe de français, car la façon d’écrire un texte en mathématiques dépend des savoirs mathématiques et pas seulement de connaissances linguistiques. On ne fait pas du français en
mathématiques, mais des mathématiques, en utilisant le français des
mathématiques. Il ne s'agit pas de juxtaposer des compétences
(mathématiques et langagières), mais ce sont leurs interactions qui permettent
une évolution dans l'abstraction … et le
rond peut enfin devenir cercle ! Hélène
Zucchetta, professeur de mathématiques en
collège ANNEXE 1 Fiches reprises de "Lire et écrire des textes mathématiques. Vers des
démonstrations" de l’IREM de
Rennes.
Voici
un programme de construction d'une même figure, rédigé de deux façons
différentes. a)
Texte élève : Je trace un segment [AB] de 4,5 cm de
long. Avec le compas, je prends un écartement de 6,5 cm. Je pointe sur le
point A. Je reprends le compas en écartant de 3 cm. Je pointe sur le point B. J'obtiens le point C et je relie A à C et B à
C. Je prends l’équerre et je place l'angle droit sur la droite (AC) je la
fais glisser jusqu'au point B et je trace la droite passant par B. b)
Texte professeur : Trace un segment [AB] de 4, 5 cm. Trace le
cercle de centre A et de rayon 6,5 cm, puis un arc de cercle de centre B et de
rayon 3 cm ; on appelle C l’un des points d'intersection. Trace les
segments [AC] et [BC]. Trace la droite perpendiculaire à la droite (AC) passant
par B.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ÉLEVE |
PROFESSEUR |
|
|
Trace un segment [AB] de 4,5 cm. |
|
Avec le compas, je prends un écartement de 6,5 cm. je le
pointe sur A. |
|
|
|
Trace un arc de cercle de centre B et de rayon 3cm. |
|
Je prends l'équerre, je place l'angle droit sur la droite
(AC), je la fais glisser jusqu'au point B et je trace la droite passant par B.. |
|
d) A ton avis, manque-t-il des consignes dans l'un des deux textes de la fiche 1 ?
e) Pour un
tracé, est-il nécessaire de donner le nom de l'instrument utilisé ?
f) Quelles
différences remarques-tu entre les deux textes ?
En Groupe :
a) Avez-vous tous obtenu la même figure
? Si non pourquoi ?
b) Pour un tracé, est-il nécessaire de
donner le nom de l'instrument utilisé ?
c) Quelles sont les différences entre les
deux textes ?
Exemple de fiche élaborée en classe
2e et 3e Séances :
Nom
date :
J'évalue mon texte de programme de construction
de figure.
Je mets une croix dans la
case qui correspond à mon texte
|
Dans mon texte de construction de
figure... |
OUI |
NON |
n° |
|
J'ai mis toutes les informations utiles à la
construction, je n’ai rien oublié. |
|
|
1 |
|
Je n'ai mis aucune information en trop. |
|
|
2 |
|
Mes consignes sont écrites dans un ordre qui permet de
refaire la figure |
|
|
3 |
|
Toutes les informations que je donne sont justes, |
|
|
4 |
|
J’ai donné les bonnes mesures, |
|
|
5 |
|
J’ai utilisé le bon codage, |
|
|
6 |
|
J'ai utilisé le vocabulaire de géométrie (ex : segment,
droite, cercle, rayon, diamètre...) |
|
|
7 |
|
J’ai écrit des phrases en utilisant les expressions de
géométrie (ex : la droite
passant par...parallèle à ... ; le
cercle de centre... et de rayon...
etc.). |
|
|
8 |
|
Mes consignes sont claires et faciles à comprendre. |
|
|
9 |
|
J’écris les phrases sans parler des instruments. |
|
|
10 |
|
J'ai mis tous les verbes au même temps et mode (ex : tous à
l'infinitif, tous à l'impératif, tous …) |
|
|
11 |
|
Je reviens à la ligne à chaque nouvelle instruction. |
|
|
12 |
|
J’ai vérifié que je ne fais pas de fautes d’orthographe
dans les mots mathématiques. |
|
|
13 |
Je note ici les numéros des
lignes auxquelles j'ai répondu "NON".
Ce sont les points sur
lesquels je dois encore m'améliorer.
|
|
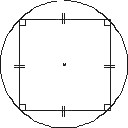
Exemples de figures proposées
Consigne : écrire un texte qui permet de refaire la figure sans
l’avoir vue.
|
|
Texte de construction de figure |
|
|
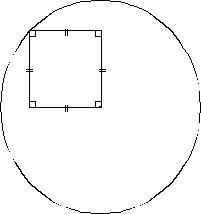
Texte de construction de figure | |
|
Texte de construction de figure |
NOM :
1e Séance :
1e
étape :
Voici un exercice pris dans le cahier
d'évaluation de début de sixième.
Fais-le au stylo. Tu ne devras rien effacer. Si tu fais une faute, barre-la proprement pour que le texte barré reste lisible.
 |
Complète le texte ci-dessous, qui doit
permettre de reproduire la figure tracée.
Trace un rectangle ABCD de longueur 8cm et de largeur 4cm.
[1] figure téléphonée : situation émetteur-récepteur où un élève décrit une figure géométrique donnée pour qu’un autre élève puisse reproduire la figure. Les consignes et la mise en place peuvent être différentes d’une situation à une autre suivant l’objectif (oralement, par écrit avec retour de questions, …)
[2] Pour nous, " faire " serait une tache d’exécution ; " faire faire " permettrait de prendre conscience d’un destinataire qui devra exécuter des instructions. Dans cette deuxième situation, la nécessité de se faire comprendre clairement et précisément, à travers les consignes, peut apparaître plus nettement au rédacteur.
[3] Cette activité est tirée de la brochure de l'IREM de Rennes intitulée "Lire et écrire des textes mathématiques. Vers la rédaction de démonstrations."
[4] par exemple, on définira le rayon du cercle par le côté du carré, et son centre par un sommet du carré.